3D 张量并行

作者: Zhengda Bian, Yongbin Li

前置教程

• 1D 张量并行
• 2D 张量并行

示例代码

• ColossalAI-Examples - 3D Tensor Parallelism

相关论文

• Maximizing Parallelism in Distributed Training for Huge Neural Networks

引言

3D 张量并行 是一种将神经网络模型的计算并行化，以期望获得最佳通信成本优化的方法。

我们还是以线性层 $Y = XA$ 为例。 给定 $P=q \times q \times q$ 个处理器（必要条件）, 如 $q=2$, 我们把输入 $X$ 和权重 $A$ 划分为

$$\left[\begin{matrix} X_{000} & X_{001} \\ X_{010} & X_{011} \\ X_{100} & X_{101} \\ X_{110} & X_{111} \end{matrix} \right] \text{~and~} \left[\begin{matrix} A_{000} & A_{001} & A_{010} & A_{011} \\ A_{100} & A_{101} & A_{110} & A_{111} \end{matrix} \right] \text{~respectively,}$$

其中每个 $X_{ijl}$ 和 $A_{lji}$ 都被存储在处理器 $(i,j,l)$ 上, 如下图所示。

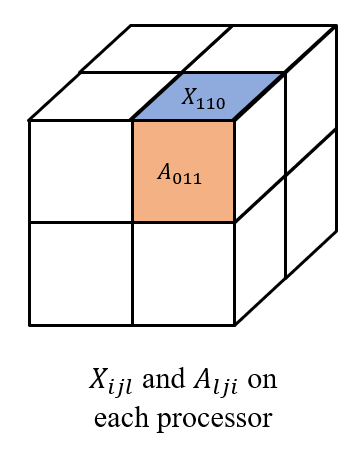
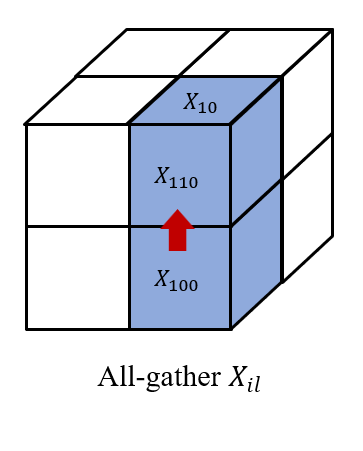
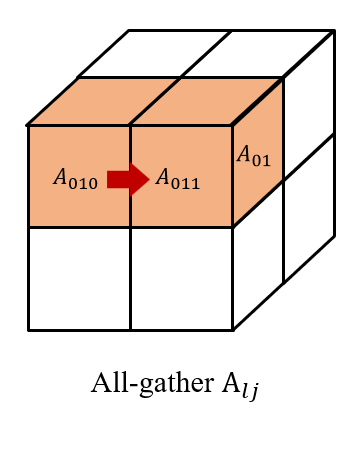
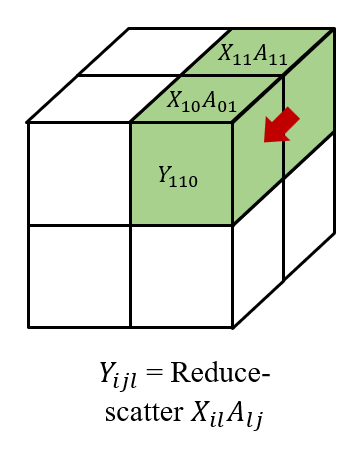
然后我们在 $(i, 0...q,l)$ 上收集 $X_{ijl}$, 以及在$(0...q, j, l)$ 上收集 $A_{lji}$。 因此，我们在每个处理器 $(i,j,l)$ 上都有 $X_{il}$ 和 $A_{lj}$ 以获得 $X_{il}A_{lj}$。 最后，我们在 $(i, j, 0...q)$ 对结果进行 reduce-scatter 得到 $Y_{ijl}$, 形成

$$Y= \left[\begin{matrix} Y_{000} & Y_{001} \\ Y_{010} & Y_{011} \\ Y_{100} & Y_{101} \\ Y_{110} & Y_{111} \end{matrix} \right].$$

我们还需要注意，在后向传播中, 我们需要 all-gather 梯度 $\dot{Y_{ijl}}$, 然后 reduce-scatter 梯度 $\dot{X_{il}}=\dot{Y_{ij}}A_{lj}^T$ and $\dot{A_{lj}}=X_{il}^T\dot{Y_{ij}}$。

效率

给定 $P=q \times q \times q$ 个处理器, 我们展现理论上的计算和内存成本，以及基于环形算法的3D张量并行的前向和后向的通信成本。

计算	内存 (参数)	内存 (activations)	通信 (带宽)	通信 (时延)
$O(1/q^3)$	$O(1/q^3)$	$O(1/q^3)$	$O(6(q-1)/q^3)$	$O(6(q-1))$

使用

ColossalAI的最新版本还暂不支持3D张量并行，但3D张量并行的功能会在未来的版本被集成入Shardformer中。关于Shardformer的原理和用法细节请参考当前目录下的Shardformer文档。

对于老版本ColossalAI的用户，3D张量并行的用法请参考ColossalAI-Examples - 3D Tensor Parallelism。