3D Tensor Parallelism

Author: Zhengda Bian, Yongbin Li

Prerequisite

• 1D Tensor Parallelism
• 2D Tensor Parallelism

Example Code

• ColossalAI-Examples - 3D Tensor Parallelism

Related Paper

• Maximizing Parallelism in Distributed Training for Huge Neural Networks

Introduction

The 3D tensor parallelism is an approach to parallelize the computation of neural models, hoping to obtain the optimal communication cost.

Let's still take a linear layer $Y = XA$ as an example. Given $P=q \times q \times q$ processors (necessary condition), e.g. $q=2$, we split the input $X$ and weight $A$ into

$$\left[\begin{matrix} X_{000} & X_{001} \\ X_{010} & X_{011} \\ X_{100} & X_{101} \\ X_{110} & X_{111} \end{matrix} \right] \text{~and~} \left[\begin{matrix} A_{000} & A_{001} & A_{010} & A_{011} \\ A_{100} & A_{101} & A_{110} & A_{111} \end{matrix} \right] \text{~respectively,}$$

where each $X_{ijl}$ and $A_{lji}$ are stored at processor $(i,j,l)$, as shown in the figure below.

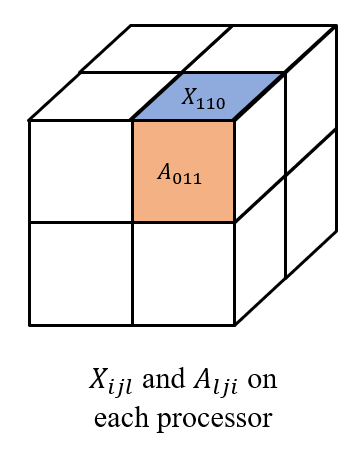
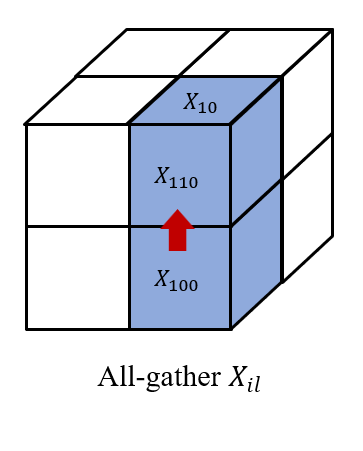
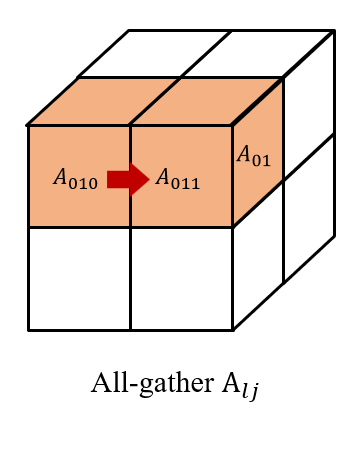
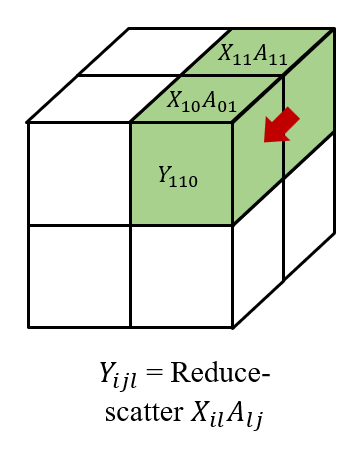
Then we all-gather $X_{ijl}$ across $(i, 0...q,l)$, as well as $A_{lji}$ across $(0...q, j, l)$. So, we have $X_{il}$ and $A_{lj}$ on each processor $(i,j,l)$ to get $X_{il}A_{lj}$. Finally, we reduce-scatter the results across $(i, j, 0...q)$ to get $Y_{ijl}$, which forms

$$Y= \left[\begin{matrix} Y_{000} & Y_{001} \\ Y_{010} & Y_{011} \\ Y_{100} & Y_{101} \\ Y_{110} & Y_{111} \end{matrix} \right].$$

We also need to note that in the backward pass, we need to all-gather the gradient $\dot{Y_{ijl}}$, and then reduce-scatter the gradient $\dot{X_{il}}=\dot{Y_{ij}}A_{lj}^T$ and $\dot{A_{lj}}=X_{il}^T\dot{Y_{ij}}$.

Efficiency

Given $P=q \times q \times q$ processors, we present the theoretical computation and memory cost, as well as the communication cost based on the ring algorithm in both the forward and backward pass of 3D tensor parallelism.

Computation	Memory (parameters)	Memory (activations)	Communication (bandwidth)	Communication (latency)
$O(1/q^3)$	$O(1/q^3)$	$O(1/q^3)$	$O(6(q-1)/q^3)$	$O(6(q-1))$

Usage

Currently the newest version of ColossalAI doesn't support 3D tensor parallelism, but this feature will be integrated into Shardformer in future releases. For more details about ideas and usages of Shardformer, please refer to Shardformer Doc.

For users of older version of ColossalAI, please refer to ColossalAI-Examples - 3D Tensor Parallelism.